Static Effect in Magnetotelluric Responses: An Implication from the EM Integral Equation

Yoonho Song

doi:10.7582/GGE.2024.27.3.181

Preview

Tutorial

Geophysics and Geophysical Exploration. 31 August 2024. 181-195
https://doi.org/10.7582/GGE.2024.27.3.181

Static Effect in Magnetotelluric Responses: An Implication from the EM Integral Equation

MT 탐사 반응에서 정적효과: 적분방정식을 통한 고찰

Yoonho Song¹^*

송 윤호¹^*

¹Deep Subsurface Storage and Disposal Research Center, Korea Institute of Geoscience and Mineral Resources

¹한국지질자원연구원 심층처분환경연구센터

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

This tutorial explains that the static effect in the magnetotelluric (MT) survey is a physical phenomenon caused by charges accumulated on the boundaries of subsurface inhomogeneities. To facilitate understanding of the physical phenomenon, differences between static induction and charge accumulation on the boundary are explained and analyzed with help of schematic illustrations. Subsequently, from the electromagnetic (EM) integral equation formulation, it is clearly shown that the secondary electric field due to charges accumulated on the interface in the presence of the primary field appears as the static effect. Therefore, except in the cases of the layered earth or a two-dimensional earth with transverse magnetic (TM) mode excitation, the static effect always exists in MT responses and further, it is not ‘static’ but rather frequency dependent.

Despite the fact that the static effect is a secondary electric field due to inhomogeneity, inevitable under-sampling in the frequency and spatial domains prevent the effect from being handled properly in numerical inversion. Therefore, considering the practical aspects of the MT survey, which cannot be a continuous measurement covering the entire survey area over a wide frequency band, a three-dimensional (3-D) inversion incorporating the static shift as a constraint with the Gaussian distribution is introduced. To enhance understanding of the integral equation EM modeling, the formulation of the 3-D integral equation and mathematical analyses of the Green tensor and scattering current are described in detail in the Appendix.

Keywords

magnetotelluric (MT) response

static effect

electromagnetic (EM)

integral equation

charge accumulation

이 해설 논문에서는 자기지전류(magnetotelluric; MT) 탐사에서의 정적효과가 지하 불균질체의 경계면에서 축적되는 전하 축적에 의해 발생하는 물리적 현상임을 설명하였다. 먼저 정적효과를 일으키는 물리적 현상에 대한 이해를 위해 정전유도와 경계면에서의 전하 축적의 차이에 대해 모식도를 이용해 설명하고 분석하였다. 그리고 적분방정식을 통해 지하에 있는 불균질체에 1차 전기장이 가해졌을 때, 전기전도도 경계면에서의 전하 축적에 의한 2차 전기장이 정적효과로 나타남을 명확히 하였다. 따라서 MT 탐사에서 1차원 층서구조나 2차원 TM (transverse magnetic) 모드의 경우를 제외하고 정적효과는 항상 존재하고 또한 그 용어와는 달리 ‘정적’이 아닌 주파수 의존적임을 보였다.

정적효과가 지하 불균질체에 의한 2차장임에도 MT 탐사의 역산에서 수식적으로 해결되지 않고 심부 구조의 해석에 장애 요인으로 작용하는 이유는 현장 탐사에서 피할 수 없는 ‘주파수 및 공간 영역에서의 과소 샘플링’이기 때문이다. 따라서 광대역 주파수와 전체 탐사 대상 면적에서의 연속 측정이 아닌 실제 MT 탐사를 고려할 때, 3차원 역산시에 정적효과를 전체 탐사 영역에서 정규분포를 갖는 변수로 가정하고 이를 역산의 제약 조건으로 포함하는 시도에 대해 알아보았다. 적분방정식 전자탐사 모델링의 이해를 돕기 위해 3차원 적분방정식의 유도, Green 텐서 및 산란전류의 수학적 분석을 부록에 자세히 서술하였다.

키워드

자기지전류(MT)탐사

정적효과

전자탐사

적분방정식

전하축적

MAIN

서 론
정전유도와 정적효과
적분방정식과 Green 텐서로부터의 정적효과 분석
현장 MT 탐사자료에서의 정적효과
결 론
부록: 전기장의 적분방정식

서 론

자기지전류(magnetotelluric; MT) 탐사는 지진파를 이용한 토모그래피와 더불어 지각 구조까지의 탐사가 가능한 대표적인 심부 탐사 방법으로 널리 알려져 있다. 특히 자연적으로 존재하는 전자기(electromagnetic; EM)장을 송신원으로 이용하기 때문에 비교적 적은 비용과 간편한 장비로도 3차원 탐사 자료 획득이 가능하며 또한 평면파(plane wave) 송신원을 가정하기 때문에 자료의 해석에서도 유리한 점이 많다. 그러나 자연 전자기장의 크기가 미약해서 잡음에 취약하고 따라서 인공 전자기 잡음이 극심한 지역에서는 의미 있는 지하의 신호 획득이 불가능하다는 단점이 있다고 알려져 있다. 이러한 단점은, 21세기 들어 전자 기기의 발달에 힘입어 넓은 동적 범위(dynamic range)를 갖는 수신기가 개발되고 인공위성을 이용한 동기화가 가능해짐에 따라 상당히 극복되어 우리나라와 같이 고도의 산업화로 인해 인공 전자기 잡음이 극심한 지역에서도 지하구조의 3차원 영상 획득이 가능해졌다(Lee et al., 2005, 2009, 2019).

광대역 주파수에 걸쳐 얻어진 임피던스 자료의 처리 및 역산을 통해 심부 지하구조를 해석하거나 영상화하는 데 있어서, 지하 천부에 존재하는 불균질체는 때때로 심부 이상체에 의한 반응을 가리는 지질학적 잡음으로 작용하는데 MT탐사에서는 이를 정적효과(static shift 또는 static effect)라 불러왔다. 이는 임피던스로부터 계산되는 겉보기 비저항이 지하 천부의 불균질체에 의해 주파수와 무관하게 로그-로그(log-log) 도표에서 수직으로 이동하는 것처럼 보이기 때문에 붙여진 이름이다. 이러한 정적효과를 제거해서 지하 심부에 의한 반응만을 추출하기 위한 시도가 오래전부터 이어져왔는데(Jang et al., 2024), 모든 경우에 완벽하게 적용되는 방법은 없다.

이와 같이 MT탐사 반응에서 정적효과를 완벽하게 제거하지 못하는 것은, 자료처리 기술이나 수치적인 영역의 문제가 아니라 정적효과 자체가 지하에서 일어나는 물리적 현상, 즉 전자기 반응이기 때문이다. 지하에 존재하는 불균질체의 깊이와 크기, 그리고 전기전도도에 따라 이에 의한 전자기 반응의 세기나 주 주파수 대역이 달라지기 때문에, 광대역 주파수 및 공간 영역에 걸쳐 정밀하게 자료를 측정해 이를 역산에 반영한다는 것은 현실적으로 어려운 문제이다. 이 해설 논문에서는 MT탐사에서의 정적효과가 지하 불균질체의 경계면에서 일어나는 전하 축적에 의한 현상임을 적분방정식의 분석을 통해 명확히 보였다. 또한 현장 탐사 자료에서의 정적효과는 ‘주파수 및 공간 영역에서의 과소 샘플링’에 의해 피할 수 없이 나타나는 현상임을 설명하고, 지하구조의 해석에 있어서 정적효과에 의한 왜곡을 적절히 피할 수 있는 방안에 대해서도 소개하였다. 적분방정식 전자탐사 모델링의 이해를 돕기 위해 3차원 적분방정식의 유도, Green 텐서 및 산란전류의 수학적 분석을 부록에 자세히 서술하였다.

정전유도와 정적효과

물리탐사에서 일반적으로 정적(static)이라 함은 시간적 또는 공간적인 변화가 없는 반응 상태를 지칭할 때 사용한다. 전자기유도 현상에 기초하는 전자탐사의 경우에는 10⁵ Hz 이하의 주파수를 대상으로 하기 때문에 변위전류의 영향을 무시해도 되는 주파수 대역의 수식화를 지칭하는 준정적 근사(quasi-static or quasi-stationary approximation)라는 용어도 통상적인 전자기학의 관심 영역에 비해 시간적 변화가 적다는 의미로 사용되고 있다. 우리의 주 관심사인 MT 탐사에서의 정적효과라는 용어 또한 MT 탐사 결과로부터 얻어지는 기본 반응인 겉보기 비저항이 주파수에 무관하게 로그-로그 도표에서 수직 이동하는 것처럼 보이기 때문에 붙여진 용어이다. 또한 공기중에 전도체가 존재할 때 발생하는 정전유도(static induction) 현상과 지표면 바로 아래에 전도체가 존재할 때 그 경계면에 축적되는 전하에 의해 발생하는 정적효과가 유사하게 보여 ‘정적(static)’이라는 의미를 연결시키게 될 수도 있다. 그러나 정전유도와 경계면에서의 전하 축적은 서로 다른 물리적 현상이다.

Fig. 1은 공기중에 전도체가 위치하고 여기에 외부에서 전기장(1차장; E₀)이 가해졌을 때 일어나는 정전유도 현상의 원리를 보여준다. 정전유도는 외부에서 가해진 전기장을 상쇄하는 방향으로 일어나는데, 이는 Coulomb의 법칙에 의해 음(–)전하는 전기장이 도달하는 방향으로 움직이고 양(+)전하는 이와 반대방향으로 움직여 결과적으로 1차장과 반대 방향으로 2차장(E_S)을 유도하기 때문이다. 전도체 표면으로 분극된 전하의 양은 Coulomb의 법칙에 따라 1차장에 비례하며 따라서 1차장을 정확히 상쇄하게 되어 전도체 내부에서는 항상 전기장이 0이 되게 된다.

(1)

E_{inside} \equiv E_{0} + E_{S} \equiv 0

이러한 정전유도 현상은 전도체의 전기전도도 크기와 무관하게 항상 발생하며 단지 완전 분극에 도달하는 시간이 전기전도도에 따라 달라질 뿐이다. 정전유도는 물리탐사, 특히 전기탐사에서 매우 중요한 의미가 있다. 대기권의 전자기 현상에 의해 지표면 위에서는 전하가 존재하게 되고 Coulomb의 법칙에 의해 땅속에는 이 전하에 의한 1차 전기장이 발생한다. 그러나 정전유도에 의해서 땅속에서는 이 1차 전기장을 상쇄시켜 그 영향이 없어지고, 따라서 인위적으로 흘려준 전기 송신원에 의한 반응만을 측정할 수 있으므로 전기탐사가 실질적으로 가능해진다(Kaufman, 1992, Section III.1).

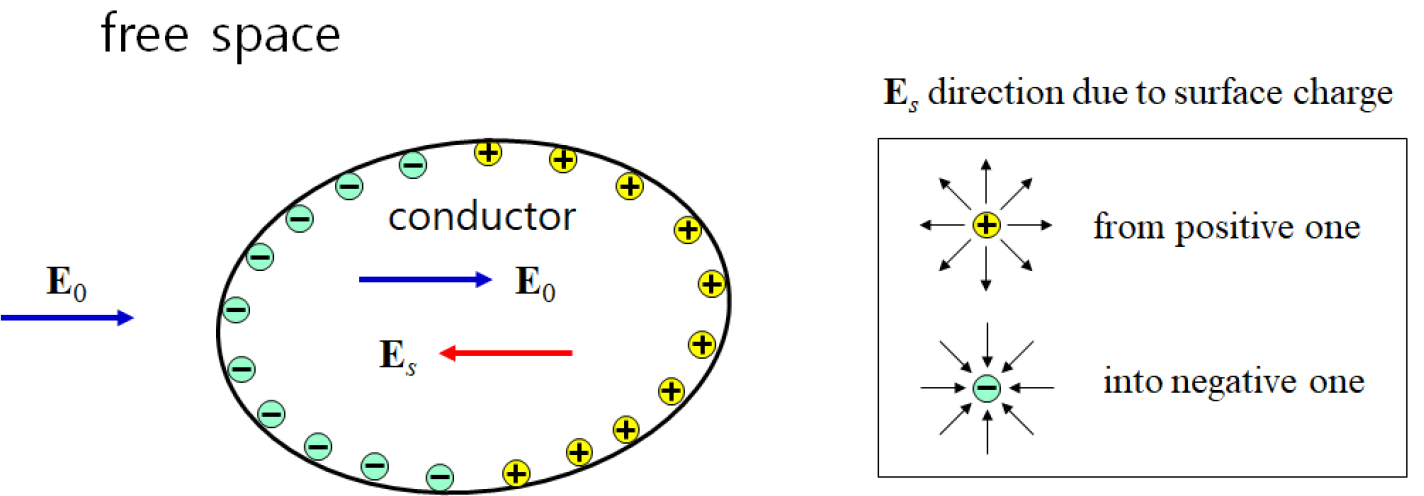
https://cdn.apub.kr/journalsite/sites/ggekseg/2024-027-03/N0540270303/images/ggekseg_27_03_03_F1.jpg

Fig. 1.

Schematic illustration showing static induction in a conductor in free space (modified from Fig. III.2 of Kaufman, 1992). E₀ is an applied electric field and E_S is the secondary field by static induction, which has equal magnitude but opposite direction to E₀, resulting that the total field vanishes in the conductor. Arrows in the right box indicate the direction of the electric fields due to Coulomb forces by positive and negative charges.

공기중이 아닌, 기본적으로 어느 정도의 전기전도도를 갖는 땅속에 위치한 이상체에서의 전기장을 생각해보자. 이 경우는 Coulomb의 법칙에 따른 앞의 정전유도와는 달리, 주어진 전기 또는 자기 송신원에 의해 흐르는 전류에 의해 발생하는(Ohm의 법칙) 1차 전기장에 대한 이상체의 반응으로 이해되어야 한다. 전기전도도 경계면에서 전류의 법선 성분(normal component)은 연속이므로 전기장의 법선 성분은 불연속일 수밖에 없으며 이러한 불연속은 경계면에 표면전하(surface charge)가 축적되어 발생하게 된다. 전기전도도가 서로 다른 매질 (1)과 매질 (2)의 경계에서 법선 벡터(normal vector)가 매질 (1)에서 매질 (2)를 향한다고 하면 전류의 법선 성분은 연속이므로

(2)

j_{n}^{(1)} = j_{n}^{2}

이 되고 여기에 Ohm의 법칙을 적용하면

(3)

\begin{aligned} j_{n}^{(2)} - j_{n}^{(1)} & = σ_{2} E_{n}^{(2)} - σ_{1} E_{n}^{(1)} \\ = \frac{1}{2} [(σ_{1} + σ_{2}) {E_{n}^{(2)} - E_{n}^{(1)}} + (σ_{2} - σ_{1}) {E_{n}^{(2)} + E_{n}^{(1)}}] \\ = 0 \end{aligned}

이 된다. Coulomb의 법칙에 의해 전기장 법선 성분의 차이가 아래와 같이 표면전하( $\sum$ )와 진공에서의 유전율(ε₀)의 비와 같으므로(Kaufman, 1992, Section III.1)

(4)

E_{n}^{(2)} - E_{n}^{(1)} = \frac{Σ}{ε_{0}}

경계면에 축적되는 표면전하는 다음과 같이 정리된다.

(5)

Σ = 2 ε_{0} \frac{σ_{1} - σ_{2}}{σ_{1} + σ_{2}} E_{n}^{a v}

여기서 법선 성분 전기장의 평균값은 아래와 같다.

(6)

E_{n}^{a v} = \frac{E_{n}^{(1)} + E_{n}^{(2)}}{2}

여기서 유념해야 할 사항은 두 매질의 전기전도도가 주어진다고 해도 표면전하의 크기를 곧 바로 구할 수 없다는 것인데, 이는 전기장 또한 전기전도도 차이에 의해 변화하기 때문에 이를 미리 알 수 없기 때문이다. 따라서 전기탐사의 경우에 면 적분방정식이나 체적 적분방정식을 구성해 그 해를 구하는 방식으로 접근하게 된다. 물론 미분방정식에 근거해 유한요소법이나 유한차분법을 통해 해를 구할 수도 있으며, 임의의 송신원과 이상체에 대해서는 어떠한 경우에도 수치적 방법으로 해를 구하게 된다.

Fig. 2는 식 (5)로 표현된 표면전하 분포와 이에 의한 전기장 변화를 모식화한 것이다. 법선 벡터가 이상체 내부를 향하므로 주변 매질(땅속)이 매질 (1)이 되고 이상체가 매질 (2)가 된다. 먼저 이상체의 전기전도도가 주변 매질보다 높은 경우(Fig. 2(a))를 보면 $σ_{1} - σ_{2} < 0$ 의 경우에 해당하고, 왼쪽 경계에서는 전기장 법선 성분의 방향과 법선 벡터의 방향이 일치하므로 표면전하는 음(–)이 될 것이고, 반대로 오른쪽 경계면에서는 전기장 법선 성분의 방향과 법선 벡터가 반대이므로 표면전하가 양(+)이 된다. 따라서 이렇게 축적된 전하에 의한 2차 전기장은 1차장과 반대방향이 될 것인데, 그 크기는 1차장보다 작을 수밖에 없다. 결과적으로 1차장과 2차장의 합인 전체 전기장은 전도성 이상체 내부에서 1차장보다 작아지게 되며 그림에 나타낸 바와 같이 이상체 주변에서는 1차장 보다 큰 부분과 작은 부분으로 나뉘게 된다.

한편 이상체의 전기전도도가 주변 매질에 비해 낮은 경우에는(Fig. 2(b)), $σ_{1} - σ_{2} > 0$ 가 되어서 앞의 경우와 정반대의 형태로 경계면에 전하가 축적되게 된다. 결과적으로 이상체 내부의 전체 전기장은 1차장보다 커지고, 또한 주변 매질에서의 전기장도 전도성 이상체의 경우와 반대 양상으로 분포하게 된다.

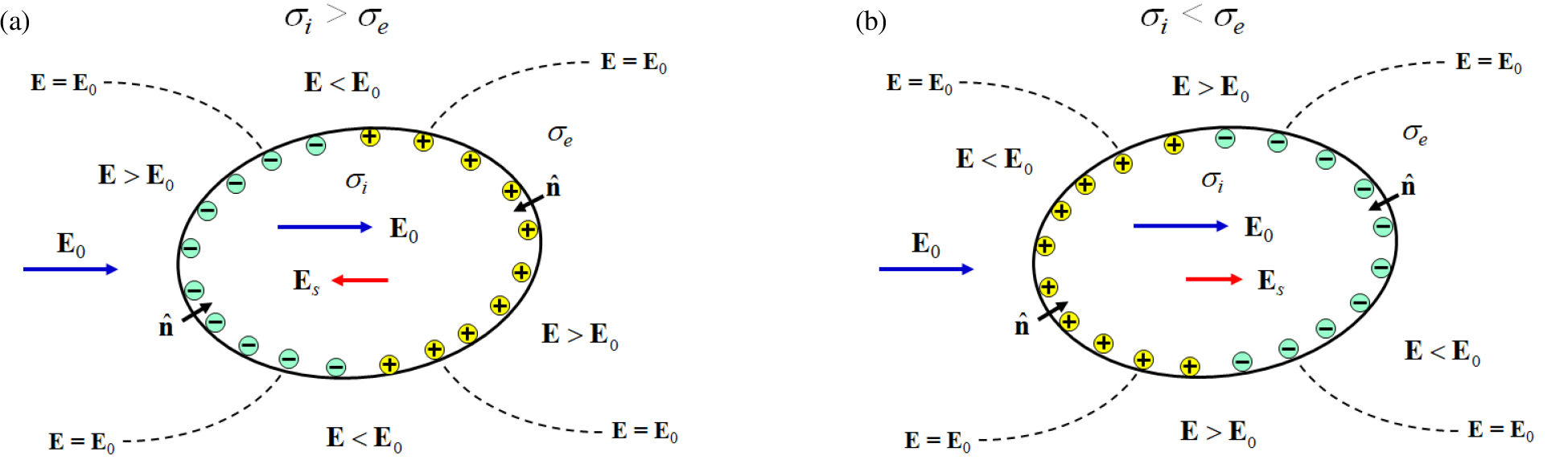
https://cdn.apub.kr/journalsite/sites/ggekseg/2024-027-03/N0540270303/images/ggekseg_27_03_03_F2.jpg

Fig. 2.

Schematic illustration showing charge accumulation at the interface between an inhomogeneity and surrounding conductive medium, and resultant distribution of the electric field for (a) conductive and (b) resistive bodies (modified from Fig. III.14 of Kaufman, 1992).

지금까지 살펴본 전기전도도 경계면에서의 전하 축적은, 전기장의 법선 성분이 불연속이라는 기본적인 전자기 현상이므로 직류 전류에 의해서만 발생하는 것이 아니고 시간에 따라 변화하는 교류 전류에서도 발생한다. 또한 이상체의 전기전도도가 주변 매질에 비해 높은 경우뿐만 아니라 낮은 경우에도 항상 발생하게 된다. 따라서 전하 축적이 정전유도 현상에서의 전하 이동(분극의 형태)과 유사한 형태처럼 보인다고 해도 이 둘은 서로 다른 물리적 현상이다. MT 탐사에서의 소위 정적효과는 이러한 전하 축적에 의한 현상이고 이는 주어진 1차장의 주파수에 따라 전자기 유도와 상대적인 크기가 달라지기 때문에 엄밀한 의미에서 ‘정적(static)’이라는 말은 물리적으로 정확하지 않은 표현이다. 그러나 MT탐사에서의 ‘정적효과’라는 용어는 이미 학계에서 널리 통용되는 표현이므로 여기서는 이를 따른다.

적분방정식과 Green 텐서로부터의 정적효과 분석

전체 공간 V 내부의 임의의 위치에 존재하는 이상체에 의한 전기장은 1차장이 주어질 때에 아래의 적분방정식으로 표현된다(부록 A, B, C). 각 기호의 설명은 부록을 참고하면 된다.

(7)

\begin{aligned} E (r) & = E_{b} (r) - \hat{z} \int_{V} \underset{―}{\underset{―}{G}} (r, r^{'}) \cdot Δ \hat{y} (r^{'}) E (r^{'}) d r^{'} \\ = E_{b} (r) - \hat{z} \int_{V} \underset{―}{\underset{―}{G}} (r, r^{'}) \cdot J_{s} (r^{'}) d r^{'} \\ = E_{b} (r) - \hat{z} \int_{V} \{(\underset{―}{\underset{―}{S}} + \frac{1}{k_{b}^{2}} \nabla Φ) \cdot (\nabla^{'} \times ψ + k_{b}^{2} \nabla^{'} ϕ)\} d r^{'} \\ = E_{b} (r) - \hat{z} \int_{V} {\underset{―}{\underset{―}{S}} \cdot \nabla^{'} \times ψ + (k_{b}^{2} \underset{―}{\underset{―}{S}} + \nabla Φ) \cdot \nabla^{'} ϕ} d r^{'} \end{aligned}

식 (7)의 첫 번째 줄은 체적 적분방정식의 원형이고, 두 번째는 Ohm의 법칙을 따라 전기장과 전도도 차이의 곱을 산란전류(scattering current)로 표시한 것이다. 한편, 세 번째는 Green 텐서를 전류 흐름 항과 경계면에서의 전하 축적(charge accumulation) 항으로, 산란전류를 맴돌이 전류(vortex current) 항과 전류 집중(current channeling) 항으로 분리한 것이며, 맴돌이 전류는 이상체 내부에만 국한되기 때문에 전하 축적을 야기하지 않음이 수학적으로 증명되어 이 부분이 사라진 형태가 네번째이다(부록 C). 이와 같이 맴돌이 전류가 완전히 전자기 유도에 의하기 때문에 전자와 후자에 의한 반응을 각각 유도 반응(inductive response)과 전류 효과(galvanic effect)로 구분해서 설명하기도 한다. 식 (B-9)로 설명된 Green 텐서 중 경계면에서의 전하 축적에 해당하는 부분이 $\nabla Φ$ 이므로 이는 곧 산란전류 중 주변 매질과 이상체를 통해 흐르는 전류 집중 항과의 내적을 통해 2차 전기장 중 전하 축적에 의한 반응이 설명됨을 잘 보여준다. 중요한 것은 전체 공간 Green 텐서에서(부록 B의 식 (B-11)) 보듯이 이 전하 축적 항은 주파수에 무관하지 않다는 것이다. 즉

(8)

\begin{aligned} \nabla Φ^{0} & = \nabla \nabla g (r - r^{'}) \\ = \nabla \nabla \frac{e^{- i k_{b} | r - r^{'} |}}{4 π | r - r^{'} |} \end{aligned}

에서 확인할 수 있는 바와 같이 지수항에 배경 매질의 전파상수가 들어있기 때문에 공기중이 아닌 한 이는 주파수에 의존적일 수밖에 없다. 준정적 근사 영역에서 전파상수는 $k_{b} = \sqrt{- i ω μ σ_{b}}$ 이므로 전하 축적 항은 주파수 의존적이며 주변 매질의 전기전도도, 주파수, 그리고 이상체의 형상에 따라 전하 축적 항과 전류 흐름 항의 상대적 크기가 달라질 뿐이다. 물론, 종래의 MT 탐사에서 관심 주파수 대역이 수백 Hz 이하여서 k_b의 크기가 거리에 비해 매우 작기 때문에 마치 직류에 의한 효과처럼 나타나 이 영향을 정적효과라고 통용하여 왔다고 볼 수 있다.

전하 축적에 대해서 조금 더 살펴보자. 전체 공간과 층서구조에서의 Green텐서는 단지 스칼라 Green 함수만 달라지기 때문에 전체 공간 성분의 분석만으로 충분하다. 식 (7)의 설명에서 전하 축적 항은 산란전류 중 전류 집중 항과의 내적을 통해 2차장의 한 부분을 생성하는 것을 확인하였다. 만약 전류의 흐름이 경계면과 평행하다면 경계면의 법선 방향과 전류 방향이 서로 직교하게 되어 이들의 내적은 0이 될 것이므로, 산란전류가 전기전도도 경계면과 평행하게만 존재한다면 전하 축적에 의한 2차장은 발생하지 않는다. 그러나 산란전류는 그 자체가 적분방정식의 해를 구하여만 알 수 있기 때문에 일반적으로 어떤 경우가 여기에 해당하는지 알 수 없다. 이를 수식적으로 살펴보면, 3차원 직교좌표계에서 전하 축적 항과 산란전류의 내적은 아래와 같다.

(9)

\begin{aligned} \nabla \nabla g (r - r^{'}) \cdot J_{s} & = (\begin{array}{c} \frac{\partial^{2}}{\partial x^{2}} \hat{i} \hat{i} + \frac{\partial^{2}}{\partial x \partial y} \hat{i} \hat{j} + \frac{\partial^{2}}{\partial x \partial z} \hat{i} \hat{k} \\ + \frac{\partial^{2}}{\partial y \partial x} \hat{j} \hat{i} + \frac{\partial^{2}}{\partial y^{2}} \hat{j} \hat{j} + \frac{\partial^{2}}{\partial y \partial z} \hat{j} \hat{k} \\ + \frac{\partial^{2}}{\partial z \partial x} \hat{k} \hat{i} + \frac{\partial^{2}}{\partial z \partial y} \hat{k} \hat{j} + \frac{\partial^{2}}{\partial z^{2}} \hat{k} \hat{k} \end{array}) g (r - r^{'}) \cdot (J_{s, x} \hat{i} + J_{s, y} \hat{j} + J_{s, z} \hat{k}) \\ = (\frac{\partial}{\partial x} \hat{i} + \frac{\partial}{\partial y} \hat{j} + \frac{\partial}{\partial z} \hat{k}) (\frac{\partial g}{\partial x} J_{s, x} + \frac{\partial g}{\partial y} J_{s, y} + \frac{\partial g}{\partial z} J_{s, z}) \end{aligned}

산란전류는 임의의 방향을 가질 수 있으므로 위 식은 3차원 구조에서는 어떠한 경우에도 전하 축적이 일어남을 보여주고 있다. 다음으로 주향(y) 방향으로 물리적 성질뿐만 아니라 입사하는 1차 전기장도 변화가 없는 2차원 MT 탐사 문제를 생각해보자. 이 경우 Green 텐서내의 벡터미분연산자는 $\nabla_{2 D} = \frac{\partial}{\partial x} \hat{i} + \frac{\partial}{\partial z} \hat{k}$ 로 단순해지기 때문에 전하 축적 항과 산란전류의 내적은 주향에 수직한 x, z성분만 남게 된다.

(10)

\begin{aligned} \nabla_{2 D} \nabla_{2 D} g (r - r^{'}) \cdot J_{s} & = (\binom{\frac{\partial^{2}}{\partial x^{2}} \hat{i} \hat{i} + \frac{\partial^{2}}{\partial x \partial z} \hat{i} \hat{k}}{+ \frac{\partial^{2}}{\partial z \partial x} \hat{k} \hat{i} + \frac{\partial^{2}}{\partial z^{2}} \hat{k} \hat{k}}) g (r - r^{'}) \cdot (J_{s, x} \hat{i} + J_{s, y} \hat{j} + J_{s, z} \hat{k}) \\ = (\frac{\partial}{\partial x} \hat{i} + \frac{\partial}{\partial z} \hat{k}) (\frac{\partial g}{\partial x} J_{s, x} + \frac{\partial g}{\partial z} J_{s, z}) \end{aligned}

따라서, Green 텐서와 산란전류의 내적은 아래와 같이 서로 결합되지 않은(uncoupled) 두 부분으로 분리되게 된다.

(11)

\begin{aligned} (\underset{―}{\underset{―}{I}} + \frac{1}{k_{b}^{2}} \nabla_{2 D} \nabla_{2 D}) g (r - r^{'}) \cdot J_{s} (r^{'}) \\ = & \{(g J_{s, x} \hat{i} + g J_{s, z} \hat{k}) + \frac{1}{k_{b}^{2}} (\frac{\partial}{\partial x} \hat{i} + \frac{\partial}{\partial z} \hat{k}) (\frac{\partial g}{\partial x} J_{s, x} + \frac{\partial g}{\partial z} J_{s, z})\} + \hat{j} g J_{s, y} \end{aligned}

그러므로 2차원 MT 탐사에서는 서로 결합되지 않은, 즉 전기장이 주향에 평행한 TE (transverse electric) 모드(mode)와 전기장이 주향에 직교하는 TM (transverse magnetic) 모드의 두 방정식으로 나뉜다. 따라서 2차원의 경우에는 서로 다른 두 개의 방정식에 기초해 해를 각각 구해야 한다는 것을 말하며 이는 적분방정식이 아니라 미분에 기초한 유한차분법이나 유한요소법을 이용하더라도 동일하다. 한편, 동일한 분석에 기초하면, 1차원 MT 탐사에서는 수평층의 경계면에서 전하 축적이 일어나지 않는다는 것을 쉽게 알 수 있다. Torres-Verdin (1991)은 이러한 현상을 공간 파수(spatial wavenumber) 영역에서 Born 근사를 이용해 분석한 바 있는데, 여기서는 근사가 아니라 3차원 적분방정식내 Green 텐서와 산란전류의 분석을 통해서 직접적으로 설명한 것이다.

한편 전자탐사에서 많은 경우에 수신기로 사용하는 코일을 이용해 자기장을 측정하는 경우를 생각해보자. Faraday의 전자기유도법칙(부록 A의 식 (A-1))을 통해 아래와 같이 자기장을 구할 수 있다.

(12)

\begin{aligned} H (r) & = - \frac{1}{\hat{z}} \nabla \times E (r) \\ = H_{b} (r) + \nabla \times \int_{V} {\underset{―}{\underset{―}{S}} \cdot \nabla^{'} \times ψ + (k_{b}^{2} \underset{―}{\underset{―}{S}} + \nabla Φ) \cdot \nabla^{'} ϕ} d r^{'} \\ = H_{b} (r) + \int_{V} {\nabla \times \underset{―}{\underset{―}{S}} \cdot \nabla^{'} \times ψ + k_{b}^{2} \nabla \times \underset{―}{\underset{―}{S}} \cdot \nabla^{'} ϕ} d r^{'} \\ = H_{b} (r) + \int_{V} \nabla \times \underset{―}{\underset{―}{S}} \cdot J_{s} (r^{'}) d r^{'} \end{aligned}

즉 자기장은 전하 축적 항을 포함하지 않는다. 물리적으로 전하 축적은 전류의 흐름을 야기하지 않고 따라서 전류가 흐르지 않으면 Ampere의 법칙에 의한 자기장이 생성되지 않는다는 것을 의미한다. 따라서 전하 축적 항은 전기장에만 영향을 미치고 이것이 지표에서 서로 직교하는 전기장과 자기장 수평 성분의 비로 정의되는 MT탐사 임피던스에서 정적효과의 형태로 나타남을 알 수 있다.

현장 MT 탐사자료에서의 정적효과

지금까지의 분석을 정리해보면, 전하 축적은 산란전류의 흐름과 전기전도도 경계면이 교차하는 경우에는 항상 2차 전기장을 발생시키게 되며 그 크기와 위상은 전기전도도 및 주파수의 함수가 된다. 따라서 이는 땅속에 존재하는 어떠한 이상체에서도 당연히 발생하는 전자기 반응의 일부이며, 또한 결코 ‘정적(static)’인 현상이 아니다. 그럼에도 이를 MT 탐사에서 정적효과라 불러왔던 이유로는 종래 MT에서 일정 간격으로 떨어진 측정점에서 천부에 존재하는 두께가 얇은 불균질체에 의해 탐사 목적인 심부의 반응이 왜곡되고, 또한 과거 측정 주파수가 수백 Hz 이하일 때에는 이러한 왜곡이 주파수에 무관한 것처럼 나타났기 때문으로 보는 것이 타당할 것이다.

그러나 두께가 얇다는 것은 상대적인 개념으로서 최근의 탐사 장비와 같이 수십 kHz까지 측정 주파수 대역이 넓어지면 두께가 수십 m인 불균질체에서도 충분히 경계면에서의 전하 축적뿐만 아니라 내부에서 전류의 흐름에 의해서도 유도 반응이 커질 수 있다. 또한 불균질체가 지표 바로 아래가 아니라 균질한 표토층 하부에 존재한다고 할지라도 수평 경계면에서 전하 축적이 발생하기만 하면 측정되는 반응에 정적효과의 형태로 영향을 미치게 됨도 쉽게 짐작할 수 있다. 단지 Fig. 2로부터 미루어 볼 수 있다시피 깊이가 증가함에 따라 그 효과가 덜 뚜렷이 보이고, 영향이 나타나는 주파수 및 수평 범위가 달라질 뿐이다. 그렇다면 MT 탐사 자료의 해석을 위한 역산(inversion)에서 수식적으로 이를 포함해서 해결할 수 있는데 왜 굳이 지금까지 이를 제거해야하는 대상으로 여겨왔을까 하는 의문이 생길 수 있다. 이는 현장에서 MT 탐사를 수행하는 방식 및 유한한 측정 주파수 대역과 관계가 있다.

MT 탐사는 지표에서 서로 직교하는 수평 전기장 2성분 및 자기장 3성분을 측정하고, 기본적으로 서로 직교하는 전기장과 자기장 수평 성분의 비로부터 임피던스를 계산하여 이를 해석한다. 자기장의 측정은 보통 유도 코일(induction coil)을 이용하므로 공간적으로 하나의 측정점으로 볼 수 있다. 그러나 전기장은 지하의 전기전도도에 따라 50~100 m 길이의 전선을 깔아 쌍극자를 만들고 그 양단에 비분극 전극을 매설하여 측정된 전위차(ΔV)를 쌍극자 길이(L)로 나누어 구하게 된다. 물론, 이때에 쌍극자 길이 내부의 전기장은 동일하다는 가정이 필수적이다. 그러나 아래 수식에서 볼 수 있듯이 물리적으로 이러한 측정은(E_dipole) 전기장을 쌍극자 길이에 걸쳐 적분한 값을 그 길이로 나누어 주는 것으로서 결과적으로 쌍극자 사이의 전기장 평균값을 구하는 것과 동일하다.

(13)

\begin{aligned} E_{dipole} & = \frac{Δ V}{L} \\ = \frac{1}{L} \int_{L} E (r) \cdot d l \end{aligned}

Fig. 3은 지표에 전도성 불연속체가 위치하는 2차원 MT 탐사에서 주향에 직교하게 전기장이 입사하였을 때(TM 모드), 지표에서 전기장의 크기(왼쪽)와 쌍극자를 이용한 측정점의 위치에 따른 측정값의 변화(오른쪽)를 모식화한 것이다. 전도성 불연속체이기 때문에 Fig. 2(a)에서와 같이 경계면에서의 전하 축적에 의해 2차장은 1차장과 반대가 될 것이므로 불연속체 상부에서의 전체 전기장(E)은 1차장(E₀)보다 작아지고 불연속체를 벗어나면 커지게 된다. 측정 주파수가 충분히 낮아 전도체 내부의 전자기 유도가 전하 축적에 비해 매우 작다고 가정한 모델이다.

오른쪽의 Fig. 3(a)의 경우 전기장 측정 쌍극자가 전도체 직상부에 존재하게 되면 당연히 측정된 전기장의 크기는 1차장보다 작아질 것이며 전형적인 정적효과의 경우가 된다. 쌍극자가 매우 길거나 또는 불균질체의 수평 크기가 작은 경우에도(Fig. 3(b)), 측정되는 전기장은 1차장보다 약간 작아질 것이며, 쌍극자가 길어질수록 1차장에 근접하게 된다. 한편, 쌍극자의 한쪽 전극만 전도체 상부에 있게 되면 그 전극의 상대적 위치에 따라 측정된 전기장이 1차장보다 크거나, 작거나 또는 비슷한 경우가 생길 것이며(Fig. 3(c)), 쌍극자가 전도체를 벗어나게 되면 1차장보다 커지고 거리가 멀어질수록 1차장에 근접할 것이다(Fig. 3(d)). 즉 전기장 측정 쌍극자의 하부뿐만 아니라 인접한 지점이라도 불균질체가 존재할 경우에는 이의 영향을 피할 수 없음을 보여준다.

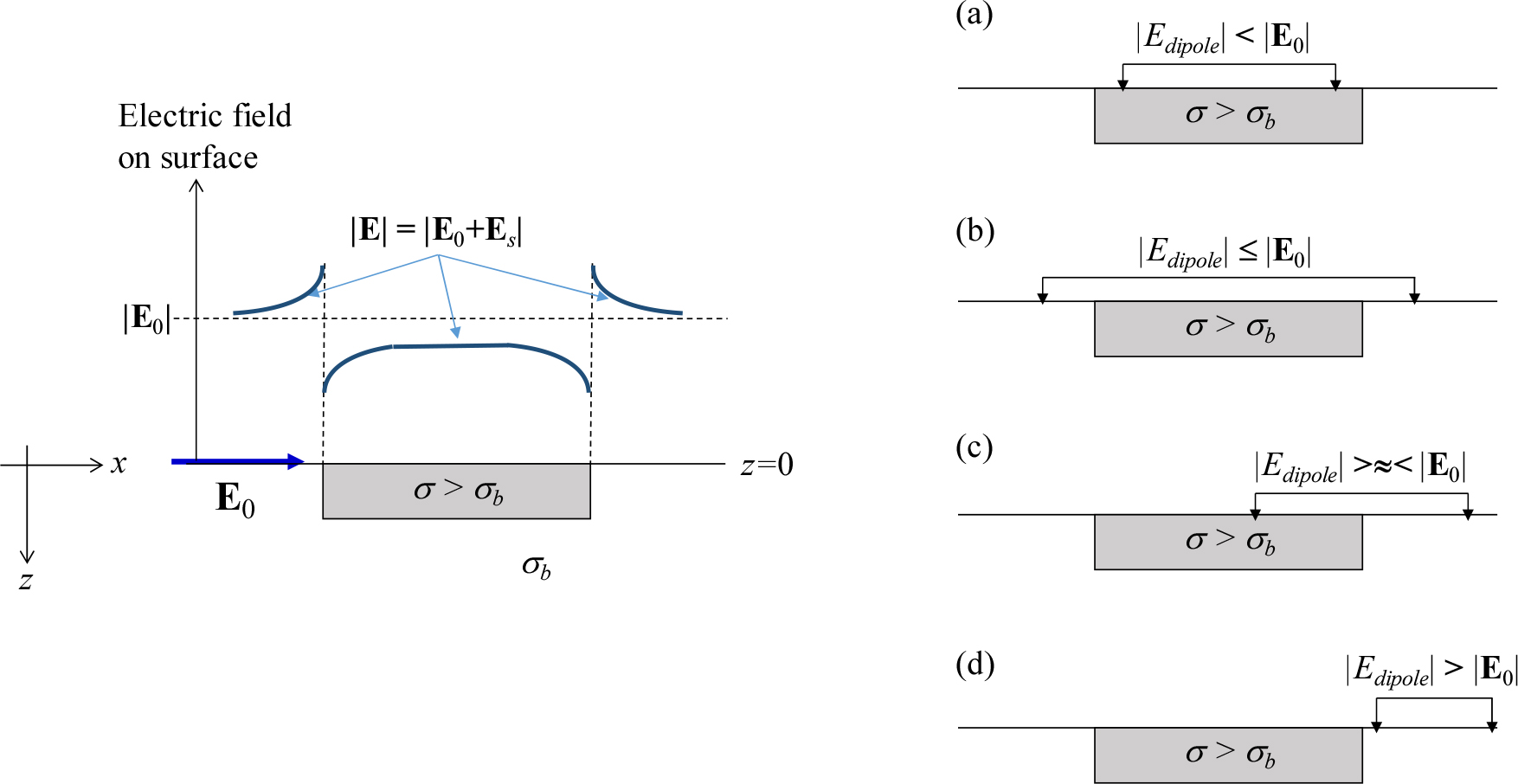
https://cdn.apub.kr/journalsite/sites/ggekseg/2024-027-03/N0540270303/images/ggekseg_27_03_03_F3.jpg

Fig. 3.

Schematic illustration showing the static effect in TM mode response for a two-dimensional earth (left) and its effect on measured electric fields (E_dipole) using a dipole at different locations relative to the superficial conductor (from (a) to (d) at right). Left panel explains the behavior of the total electric field on the surface (E), which is larger than the incident field (E₀) outside of the conductor but smaller than E₀ over the conductor due to charge accumulation at the interface.

이와 같이 지표 바로 아래 또는 천부에 불균질체가 존재할 경우에 MT 탐사의 전기장 측정 방식으로는 전하 축적에 따른 정적효과에 의해 지하 심부에 의한 반응이 왜곡되는 현상을 피할 수 없다. 이러한 영향을 효과적으로 억제하고자 제안된 방법이 측선 진행 방향으로 전기장 측정 쌍극자가 연속되게 측정을 하고 결과적으로 얻어진 측선-주파수 축으로 이루어진 임피던스 단면에 주파수에 따라 길이가 달라지는 공간 저주파 통과 필터(spatial low-pass filter)를 적용하는 EMAP (electromagnetic array profiling) 탐사법이다(Torres-Verdin and Bostick, 1992). 이 방법은 TM 모드 2차원 MT 탐사에서 필연적으로 나타나는 정적효과에 대한 올바른 물리적 분석에 기초하고 있기 때문에, 완벽하게 정적효과를 제거하지는 못하더라도, 실제 현장에서 유용한 결과를 제공할 수 있으며 우리나라에서도 성공적으로 적용된 바 있다(Kwon et al., 2006).

한편, 지하구조의 3차원 영상화를 위한 3차원 탐사에서는 현실적으로 전체 탐사영역에서 이와 같은 연속적인 탐사를 수행하는 것이 불가능에 가깝다. 더욱이 지하 심부의 이상체는 그 직상부뿐만 아니라 충분히 떨어진 곳에서도 MT 반응에 영향을 미치게 된다는 점과, 서로 직교하는 두 방향 성분(TE 와 TM 모드)을 측정해서 해석하는 MT 탐사의 특성을 고려한다면 굳이 연속적으로 전기장을 측정하지 않더라도 지하 심부에 의한 반응을 해석할 수 있어야 한다. 따라서 3차원 영상화 문제는 어떻게 자료 해석단계에서 천부 불균질체에 의한 정적효과를 억제 혹은 제거하느냐로 귀결된다고 할 수 있는데, 정적효과를 다룬 여러 연구를 분석한 결과를 보면(Jang et al., 2024) 많은 경우에 보정(correction)을 통해 심부의 반응 만을 추출하는 접근 방식을 채택하고 있다. 그러나 이론적으로 살펴본 바와 같이 정적효과는 지하 불균질체의 경계면에 축적되는 전하에 의한 물리적 반응으로 주파수와 전기전도도의 함수이기 때문에 완벽하게 제거하거나 보정하는 것은 불가능할 것이다.

이를 다르게 표현한다면, MT 탐사 자료에 나타나는 정적효과가, Vozoff (1991, p. 666)가 일찍이 설파한 바와 같이 “주파수 및 공간 영역에서의 과소 샘플링(under-sampling)에 기인”하기 때문인데, 이를 고려한다면 해석단계에서 정적효과를 ‘충분히 측정되지 않은’ 독립변수로 간주하여 처리하는 방안을 생각해볼 수 있다. 지표에서만 반응을 측정하는 MT 탐사의 경우, 깊이가 증가할 수록 해상도는 줄어들 수 밖에 없고 지표에서조차도 연속적으로 측정할 수 없으며, 사용 주파수 또한 유한하기 때문에 역산에서 ‘충분히 측정되지 않은 과소 샘플링 문제’를 완벽하게 고려할 수 없기 때문이다. 정적효과를 독립변수로 간주하여 의미있는 결과를 얻는 하나의 방법으로는 Sasaki (2004)가 제안한, 정적효과를 전체 합이 0인 정규분포를 따르는 정적 변수로 가정하여 역산의 제약(constraint) 조건에 추가한 3차원 MT 탐사 자료 역산법이 있다. 이 방법을 이용하면 이론 자료뿐만 아니라 현장 자료에 대해서도 매우 안정적이고 의미있는 3차원 역산 결과를 얻을 수 있으며, 우리나라에서 수행한 3차원 MT 탐사 자료의 역산에서도 성공적으로 적용된 바 있다(Lee et al., 2005, 2009, 2019). 물론 이 경우에도 정적효과의 주파수 의존성까지 포함하지는 못하고 있으나, 어떠한 경우에도 ‘주파수 및 공간영역에서의 과소 샘플링’ 문제를 극복할 수 없다는 점을 감안하면 Sasaki (2004)가 제시한 역산법이 현실적으로 채택할 수 있는 좋은 대안으로 볼 수 있다.

결 론

MT 탐사 자료를 이용하여 지하 심부 구조를 해석할 때, 정적효과는 자료 해석의 오류를 유발할 수 있는 큰 장애 요소이며 특히 3차원 지하구조 영상화에서 그 영향이 심각하다. 오랜 기간 동안 정적효과의 효과적인 제거를 위한 연구가 지속되어 왔지만 아직까지 확실한 해결책이 나와있지 않다. 이 논문에서는 정적효과가 단순히 잡음으로서 제거될 수 없는 현상임을 전자탐사 적분방정식에 근거해 분석하였다.

먼저 정적효과를 일으키는 물리적 현상에 대한 이해를 위해 정전유도와 경계면에서의 전하 축적의 차이에 대해 모식도를 이용해 설명하고 분석하였다. 그리고 적분방정식을 통해 지하에 있는 불균질체에 1차 전기장이 가해졌을 때, 2차장은 전류의 흐름과 경계면에서의 전하 축적에 의해 생성됨을 알아보았다. 이 중 전하 축적은 전기장이 전도도 경계면과 교차할 때에는 항상 발생하며 이에 의한 2차 전기장이 정적효과로 나타난다. 따라서 MT 탐사에서 1차원 층서구조나 2차원 TM 모드의 경우를 제외하고 정적효과는 항상 존재하며, 그 용어의 명칭과는 달리 ‘정적’이 아닌 주파수 의존적이란 것을 적분방정식을 통해 명확히 설명하였다.

정적효과가 지하 불균질체에 의한 2차장임에도 MT 탐사의 역산에서 수식적으로 해결되지 않고 심부 구조의 해석에 장애 요인으로 작용하는 이유는 현장 탐사에서 피할 수 없는 ‘주파수 및 공간 영역에서의 과소 샘플링’이기 때문을 수식에 추가한 모식도를 이용해서 확인할 수 있다. 따라서 광대역 주파수와 전체 탐사 대상 면적에서의 연속 측정이 아닌 실제 MT 탐사에서 이러한 필연적 한계로 인해 역산에서는 정적효과가 정확히 고려되지 못한다. 이에 대한 해결 방안의 하나로 정적효과를 전체 탐사 영역에서 정규분포를 갖는 변수로 가정하고 이를 역산의 제약 조건으로 포함하는 시도에 대해서 알아보았고, 이러한 방법은 정적효과의 주파수 의존성을 정확히 반영하지는 못하지만 실제 탐사자료의 역산에서 의미있는 결과를 제공하는 하나의 대안이다. 앞으로 더 많은 연구가 이루어져 좀 더 강력한 해석 방법이 나올 수 있기를 기대한다.

이 논문에서 서술한 정적효과 분석에 대한 접근 방식이 유일한 방법은 아닐 것이며 또한 가장 좋은 표현이 아닐 수 있다. 그러나 전기장 적분방정식 자체가 지하 이상체에 의해 일어나는 전자기 반응, 즉 2차장을 산란전류와 Green 텐서 내적의 적분으로 표현하는 만큼 물리적 현상에 대한 직접적 이해를 돕는데 유리할 것이다. 따라서 MT 탐사뿐만 아니라 유한 송신원을 이용한 전자탐사 반응의 이해에도 도움을 줄 것이라 믿는다. 또한 부록에서 자세히 서술한 적분방정식의 유도 및 부가적인 변수의 수학적 표현이 전자탐사 문제의 올바른 이해에 도움이 되길 기대한다.

Acknowledgements

이 논문은 한국지질자원연구원 기본사업 ‘심지층 개발과 활용을 위한 지하심부 특성평가 기술 개발’과제(GP2020-010) 수행의 일환으로 작성되었다. 논문의 서술이 좀 더 이해하기 쉽게 다듬어질 수 있도록 유익한 조언을 해주신 심사위원께 감사드린다.

부록: 전기장의 적분방정식

A. 3차원 체적 적분방정식의 유도

시간의존성을 $e^{+ i ω t}$ 라 할 때, 주파수영역에서 전류송신원에 의한 Maxwell 방정식은 아래와 같이 정리된다.

(A-1)

\nabla \times E (r) + i ω μ H (r) = 0

(A-2)

\nabla \times H (r) - {σ (r) + i ω ε (r)} E (r) = J_{e} (r)

(A-3)

\nabla \cdot B (r) = 0

(A-4)

\nabla \cdot D (r) = ρ (r)

여기서 $r$ 은 위치 벡터(단위: m), $E$ 는 전기장(단위: V/m), $H$ 는 자기장(단위: A/m), $B$ 는 자기유도(단위: Wb/m² 또는 Tesla), $D$ 는 변위전류(단위: C/m²), $μ$ 는 투자율(MT를 포함한 전자탐사에서 투자율은 진공에서의 값 $μ_{0} = 4 π \times 10^{- 7}$ H/m과 같다고 가정), $σ$ 는 전기전도도(단위: S/m), $ε$ 은 유전율(단위: F/m), $ω$ 는 각 주파수(단위: Hz), $ρ$ 는 전하밀도이다(단위: C/m³). $J_{e}$ 는 전류송신원으로서, $r_{s}$ 에 위치하고 방향 ${\hat{i}}_{s}$ , 모멘트 $I d l$ (전류 × 길이)을 갖는 쌍극자를 상정하면 아래와 같이 표현될 수 있으며, 여기서 $δ (r - r_{s})$ 는 Dirac delta함수이다.

(A-5)

J_{e} (r) = {\hat{i}}_{s} I d l δ (r - r_{s})

또한 자기유도, 그리고 전류밀도( $J$ ; 단위: A/m²)와 변위전류는 아래의 법칙에 의해 각각 자기장 및 전기장과 연결되는데, 전류밀도와 전기장의 관계는 Ohm의 법칙이다.

(A-6)

B = μ H

(A-7)

J = σ E

(A-8)

D = ε E

자기송신원을 가정하면 Faraday의 전자기유도법칙의 미분 형태 표현인 식 (A-1) 또한 송신원을 포함하는 것으로 표현할 수 있지만, 자기송신원은 언제든지 전기송신원의 적절한 변환을 통해 나타낼 수 있으므로 전기송신원만을 고려해도 전자탐사 문제를 정리할 수 있다. 식 (A-2)의 자기장에 식 (A-1)을 대입하면 아래와 같은 전기장의 파동방정식을 얻게 되는데,

(A-9)

\nabla \times \nabla \times E (r) - k^{2} (r) E (r) = - \hat{z} J_{e} (r)

여기서 전파상수(propagation constant) $k$ 는 impedivity ( $\hat{z} = i ω μ$ )와 admittivity ( $\hat{y} = σ + i ω ε$ )가 결합된 형태로서 아래와 같다.

(A-10)

\begin{aligned} k^{2} (r) & = - \hat{z} \hat{y} (r) \\ = - i ω μ {σ (r) + i ω ε (r)} \end{aligned}

MT 탐사를 포함한 대부분의 전자탐사 문제에서와 같이 사용 주파수가 10⁵ Hz 이하로서 변위전류의 영향을 무시할 수 있는 준정적 근사 영역에서 admittivity는 전기전도도로 단순화되어 전파상수의 제곱 또한 $k^{2} (r) = - i ω μ σ (r)$ 로 간단해진다. 식 (A-9)의 파동방정식으로부터, 임의 위치 r에서의 전기장을 표현하는 적분방정식을 얻기 위한 첫 번째 단계로서 아래의 식을 만족하는 Green 텐서를 도입한다.

(A-11)

\nabla \times \nabla \times \underset{―}{\underset{―}{G}} (r, r^{'}) - k_{b}^{2} \underset{―}{\underset{―}{G}} (r, r^{'}) = \underset{―}{\underset{―}{I}} δ (r - r^{'})

물리탐사 문제의 공식에 자주 동원되는 Green 함수의 정의에서와 같이, Green 텐서의 요소 $G_{i j}$ 는 $r^{'}$ 에 위치하고 $j$ 방향을 향하는, 모멘트가 $- \frac{1}{\hat{z}}$ 인 전기쌍극자 송신원에 의한 $r$ 에서의 $i$ 방향 전기장을 나타낸다. $k_{b}$ 는 배경 전파상수로서 Green 텐서를 어떻게 정의하는 가에 따라 전체 공간(예를 들어 공기중), 반무한 공간, 또는 층서구조에서의 물성으로 나타낼 수 있게 된다. $\underset{―}{\underset{―}{I}}$ 는 단위 텐서(identity tensor)로서 요소 $I_{i j}$ 는 $i = j$ 일 때만 1의 값을 갖고 나머지 요소는 0이다. 한편, Green 텐서는 대칭 텐서이고 상반성의 원리(reciprocity principle)를 만족하므로 수식적으로는 아래와 같이 표현할 수 있다(Tai, 1994, Section 4-4, 4-5).

(A-12)

\underset{―}{\underset{―}{G}} (r, r^{'}) = {[\underset{―}{\underset{―}{G}} (r^{'}, r)]}^{T}

식 (A-9) 각 항의 뒷부분에 $\underset{―}{\underset{―}{G}} (r, r^{'})$ 를 내적하고, 식 (A-11) 각 항의 앞부분에 $E (r)$ 를 내적한 후에 이를 빼주는 과정은 아래와 같다.

(A-13)

\nabla \times \nabla \times E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) - k^{2} (r) E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) = - \hat{z} J_{e} (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'})

(A-14)

E (r) \cdot \nabla \times \nabla \times \underset{―}{\underset{―}{G}} (r, r^{'}) - {k_{b}}^{2} E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) = E (r) \cdot \underset{―}{\underset{―}{I}} δ (r - r^{'})

(A-15)

\begin{aligned} \nabla \times \nabla \times E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) - E (r) \cdot \nabla \times \nabla \times \underset{―}{\underset{―}{G}} (r, r^{'}) - Δ k^{2} (r) E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) \\ = - \hat{z} J_{e} (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) - E (r) \cdot \underset{―}{\underset{―}{I}} δ (r - r^{'}) \end{aligned}

여기서 $Δ k^{2} (r) = k^{2} (r) - k_{b}^{2} = - \hat{z} Δ \hat{y} (r)$ 이다. 식 (A-15)를 전체 공간 $V$ 에 대해 적분해보자. 먼저, 우변의 첫 번째 항은 아래와 같이 이상체가 존재하지 않을 때의, 즉 배경 매질에 의한 1차장으로 정리된다.

(A-16)

\begin{aligned} \int_{V} - \hat{z} J_{e} (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) d r & = - \hat{z} \int_{V} \underset{―}{\underset{―}{G}} (r^{'}, r) \cdot J_{e} (r) d r \\ = - \hat{z} \int_{V} \underset{―}{\underset{―}{G}} (r^{'}, r) \cdot {\hat{i}}_{s} I d l δ (r - r_{s}) d r \\ = - \hat{z} I d l \underset{―}{\underset{―}{G}} (r^{'}, r_{s}) \cdot {\hat{i}}_{s} \\ = E_{b} (r^{'}) \end{aligned}

다음으로, 식 (A-15)의 우변 두 번째 항 역시 Dirac delta함수의 정의로부터 아래와 같이 위치 $r^{'}$ 에서의 전기장이 된다.

(A-17)

\int_{V} - E (r) \cdot \underset{―}{\underset{―}{I}} δ (r - r^{'}) d r = - E (r^{'})

이제 식 (A-15)의 좌변에 대한 적분을 생각해보자. 첫 번째와 두 번째 항은 벡터-다이아딕 관계식 $\nabla \cdot (a \times \underset{―}{\underset{―}{b}}) = (\nabla \times a) \cdot \underset{―}{\underset{―}{b}} - a \cdot (\nabla \times \underset{―}{\underset{―}{b}})$ )에 기초한 벡터-다이아딕 Green 정리를 통해 아래와 같이 표현된다.

(A-18)

\begin{aligned} \begin{aligned} \int_{V} {\nabla \times \nabla \times E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) - E (r) \cdot \nabla \times \nabla \times \underset{―}{\underset{―}{G}} (r, r^{'})} d r \end{aligned} \\ = & \int_{V} [\begin{matrix} \nabla \cdot \{\nabla \times E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'})\} + \nabla \times E (r) \cdot \{\nabla \times \underset{―}{\underset{―}{G}} (r, r^{'})\} \\ + \nabla \cdot \{E (r) \times \nabla \times \underset{―}{\underset{―}{G}} (r, r^{'})\} - \nabla \times E (r) \cdot {\nabla \times \underset{―}{\underset{―}{G}} (r, r^{'})} \end{matrix}] d r \\ = & \int_{V} \nabla \cdot {E (r) \times \nabla \times \underset{―}{\underset{―}{G}} (r, r^{'}) + \nabla \times E (r) \times \underset{―}{\underset{―}{G}} (r, r^{'})} d r \end{aligned} = \oint_{s} \hat{n} \cdot {E (r) \times \nabla \times \underset{―}{\underset{―}{G}} (r, r^{'}) + \nabla \times E (r) \times \underset{―}{\underset{―}{G}} (r, r^{'})} d S

전기장은 전체 공간에서 유한하고 Green 텐서는 무한 경계에서 0이 되므로 결과적으로 식 (A-18)은 0이 된다. 따라서, 식 (A-16), (A-17) 및 (A-18)을 합치면 식 (A-15)의 전체 공간 $V$ 에 대한 적분은 아래와 같이 되는데,

(A-19)

E (r^{'}) = E_{b} (r^{'}) + \int_{V} Δ k^{2} (r) E (r) \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) d r

여기서 $r$ 과 $r^{'}$ 을 서로 바꾸고 상반성의 원리를 이용하여 정리하면 $r, r^{'} \in V$ 영역에서 아래와 같은 제2종 Fredholm 적분방정식을 얻게 된다. 우변의 첫 번째가 배경 매질에 의한 1차장이고 두 번째의 적분항이 이상체가 존재할 때에만 값을 갖는 2차장이므로 전기장은 항상 1차장과 2차장의 합으로 표현된다.

(A-20)

E (r) = E_{b} (r) - \hat{z} \int_{V} \underset{―}{\underset{―}{G}} (r, r^{'}) \cdot Δ \hat{y} (r^{'}) E (r^{'}) d r^{'}

위 식에서 전체 전기장이 좌변뿐만 아니라 우변의 적분항에도 포함되어 나타나므로 일반적으로 이의 해석적 해는 존재하지 않는다. 따라서 이상체를 충분히 작은 크기로 분할하고 그 미소체 내에서는 전기장이 일정하다는 가정을 도입해서 적분항 밖으로 꺼낸 후, Green 텐서만의 수치 적분이 포함된 행렬식을 구성해 수치적으로 해를 구하는 것이 일반적이다(Hohmann, 1987). 한편, 식 (A-20)은 Ohm의 법칙에 따라 산란전류(scattering current) $J_{s} (r^{'}) = Δ \hat{y} (r^{'}) E (r^{'})$ 의 개념을 이용하면 아래와 같이도 표현할 수 있다.

(A-21)

E (r) = E_{b} (r) - \hat{z} \int_{V} \underset{―}{\underset{―}{G}} (r, r^{'}) \cdot J_{s} (r^{'}) d r^{'}

수치적으로 적분방정식의 해를 구하는 방법을 살펴본다. 예를 들어 직육면체 형태의 3차원 이상체를 그 내부에서의 전기장 또는 산란전류가 동일한 $N$ 개의 미소체로 분할한다고 가정해보자. 이 경우 $m$ 번째 미소체에서의 산란전류는 식 (A-21)에서

(A-22)

\frac{1}{Δ {\hat{y}}_{m}} J_{s}^{m} = E_{b}^{m} + \sum_{n = 1}^{N} {\underset{―}{\underset{―}{Γ}}}_{m n} \cdot J_{s}^{n}

와 같이 근사할 수 있을 것이고 여기서 ${\underset{―}{\underset{―}{Γ}}}_{m n}$ 은 미소체에 대한 Green 텐서의 적분으로 아래와 같으며, 이 또한 일반적으로 수치 적분을 통해 구한다.

(A-23)

{\underset{―}{\underset{―}{Γ}}}_{m n} = - \hat{z} \int_{V_{n}} \underset{―}{\underset{―}{G}} (r_{m}, r^{'}) d r^{'}

식 (A-22)는 아래와 같이 정리되고

(A-24)

\sum_{n = 1}^{N} \{\frac{1}{Δ {\hat{y}}_{m}} δ_{m n} \underset{―}{\underset{―}{I}} - {\underset{―}{\underset{―}{Γ}}}_{m n}\} \cdot J_{s}^{n} = E_{b}^{m}

여기서 $δ_{m n}$ 는 Kronecker delta로서 $m = n$ 일 때만 1의 값을 갖고 아닌 경우에는 0이다. 따라서 전체 $N$ 개의 미소체에서는 아래와 같은 행렬식으로 정리되어 결과적으로 적분방정식의 수치 해를 구하는 것은 이 행렬식을 푸는 문제가 된다. 3차원 공간이므로 임피던스 행렬 $\underset{―}{\underset{―}{Z}}$ 는 $3 N \times 3 N$ 의 꽉찬 행렬(full matrix)이 된다.

(A-25)

\underset{―}{\underset{―}{Z}} \cdot J_{s} = E_{b}

B. Green 텐서

Green 텐서는 전체 공간(공기중)이나, 반무한 공간, 또는 층서구조를 나타낼 수 있도록 정의할 수 있는데(부록 A), 여기서는 일반적인 물리탐사 문제에 적합하도록 배경 매질이 반무한 공간이나 층서구조인 경우를 생각해 본다. 보통 Green 텐서의 각 요소는 TM 및 TE 모드 포텐셜을 이용해 경계면에서 전기장 및 자기장 접선 성분이 연속이라는 경계조건을 적용함으로써 구하게 된다. 층서구조를 생각할 때, Green 텐서는 아래와 같이 전체 공간 성분과 층서구조 성분의 합으로 나타낼 수 있다.

(B-1)

\underset{―}{\underset{―}{G}} (r, r^{'}) = {\underset{―}{\underset{―}{G}}}^{0} (r, r^{'}) + {\underset{―}{\underset{―}{G}}}^{1} (r, r^{'})

전체 공간의 Green 텐서 ${\underset{―}{\underset{―}{G}}}^{0} (r, r^{'})$ 는 포텐셜을 이용하지 않고 다음의 과정을 통해 쉽게 구할 수 있다(Tai, 1994, Section 4-2). 식 (A-11)에 발산(divergence)을 취하게 되면

(B-2)

\begin{aligned} \nabla \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) & = - \frac{1}{k_{b}^{2}} \nabla \cdot \underset{―}{\underset{―}{I}} δ (r - r^{'}) \\ = - \frac{1}{k_{b}^{2}} \nabla δ (r - r^{'}) \end{aligned}

가 되고, 식 (A-11)은 아래와 같이 풀어서 쓸 수 있으므로

(B-3)

- \nabla^{2} \underset{―}{\underset{―}{G}} (r, r^{'}) + \nabla \nabla \cdot \underset{―}{\underset{―}{G}} (r, r^{'}) - k_{b}^{2} \underset{―}{\underset{―}{G}} (r, r^{'}) = \underset{―}{\underset{―}{I}} δ (r - r^{'})

식 (B-2)를 (B-3)에 대입하면 아래 식으로 정리된다.

- (\nabla^{2} + k^{2}) \underset{―}{\underset{―}{G}} (r, r^{'}) - \frac{1}{k_{b}^{2}} \nabla \nabla δ (r - r^{'}) = \underset{―}{\underset{―}{I}} δ (r - r^{'})

또는

(B-4)

(\nabla^{2} + k^{2}) \underset{―}{\underset{―}{G}} (r, r^{'}) = - (\underset{―}{\underset{―}{I}} + \frac{1}{k_{b}^{2}} \nabla \nabla) δ (r - r^{'})

이 식은 전체 공간 및 층서구조 성분 각각에도 성립하므로, 전체 공간의 Green 텐서 ${\underset{―}{\underset{―}{G}}}^{0} (r, r^{'})$ 이 아래와 같은 형태라고 하고

(B-5)

{\underset{―}{\underset{―}{G}}}^{0} (r, r^{'}) = (\underset{―}{\underset{―}{I}} + \frac{1}{k_{b}^{2}} \nabla \nabla) g (r - r^{'})

이를 식 (B-4)에 대입하면

(B-6)

(\underset{―}{\underset{―}{I}} + \frac{1}{k_{b}^{2}} \nabla \nabla) {(\nabla^{2} + k_{b}^{2}) g (r - r^{'}) + δ (r - r^{'})} = 0

이 되는데, 이 식이 항상 성립하기 위해서는 두 번째 괄호 항이 0이 되어야 하므로, $g (r - r^{'})$ 은 아래 식 (B-7)을 만족해야 하고, 이 식의 해는 식 (B-8)과 같이 잘 알려진 전체 공간에서의 스칼라 Green 함수이다.

(B-7)

\begin{aligned} (\nabla^{2} + k_{b}^{2}) g (r - r^{'}) = - δ (r - r^{'}) \end{aligned}

(B-8)

g (r - r^{'}) = \frac{1}{4 π} \frac{e^{- i k_{b} | r - r^{'} |}}{| r - r^{'} |}

층서구조에 대한 Green 텐서 또한 식 (B-4)를 만족해야 하므로 Green 텐서는 항상 식 (B-5)와 같이 두 텐서 성분의 합으로 표현됨을 알 수 있는데, 첫 번째는 전류에 의한 반응을 나타내는 항이고, 두 번째는 경계면에서 전하 축적에 의한 반응을 의미한다.

(B-9)

\underset{―}{\underset{―}{G}} (r, r^{'}) = \underset{―}{\underset{―}{S}} + \frac{1}{k_{b}^{2}} \nabla Φ

여기서 전류에 의한 항과 전하 축적에 의한 항은 전체 공간에서 각각 다음과 같다.

(B-10)

\begin{aligned} {\underset{―}{\underset{―}{S}}}^{0} = \underset{―}{\underset{―}{I}} g (r, r^{'}) = \underset{―}{\underset{―}{I}} \frac{e^{- i k_{b} | r - r^{'} |}}{4 π | r - r^{'} |} \end{aligned}

(B-11)

\begin{aligned} Φ^{0} = \nabla g (r - r^{'}) \end{aligned}

식 (B-9)에서 전하 축적 항에 붙어있는 $\frac{1}{k_{b}^{2}}$ 은 배경 매질의 전기전도도가 낮거나 주파수가 낮아짐에 따라 값이 커지게 되므로, 적분방정식 모델링에서 수치적으로 불안해짐으로써 수치 모델링의 큰 제약 요소로 작용한다.

C. 산란전류의 분석

적분방정식에 기초한 모델링에서 수치적 불안정성(부록 B)을 극복하는 방법의 하나로, 산란전류를 물리적으로 분석해보자. 이는 적분방정식을 이용한 수치 모델링의 안정성 확보와 더불어, 산란전류를 물리적으로 분석하는 것 자체가 전자탐사에서 2차장의 거동을 좀 더 잘 이해할 수 있기 때문이다. 적분방정식에서 산란전류의 분석을 이용해 수치적 안정성을 확보하는 방식은 얇은 판상 전도체(thin sheet)에 대해서 Weidelt (1981)가 시도한 이래로 Song et al. (2002)이 수백 MHz의 고주파수 대역까지 확대 적용한 바 있다.

기본 개념은 산란전류에, 모든 벡터는 발산이 0인 (divergence-free) 항과 회전(curl)이 0인 (curl-free) 항의 합으로 표현된다는 Helmholtz 정리를 적용하는 것이다.

(C-1)

J_{s} = \nabla \times ψ + k_{b}^{2} \nabla φ

여기서 $\nabla \times ψ$ 는 발산이 0인 맴돌이 전류(vortex current)를 나타내고, $k_{b}^{2} \nabla φ$ 은 회전이 사라지는 전류집중(current channeling)항을 말한다. 물리적으로 맴돌이 전류 항은 전도성 이상체 내부에만 존재하는 반면, 전류집중 항은 전도성 이상체를 통해 전류가 더 많이 흐르도록 배경 전류의 흐름을 변화시키는 부분을 설명하므로 여기에 전파상수의 제곱을 붙이는 것이 타당하다. 예를 들어 전기전도도가 0인 공기중에 전도체가 존재한다고 가정해보자. 이 경우, $k_{b} = 0$ 이 되므로 식 (C-1)의 산란전류는 주변 매질과의 전류 흐름은 없이 온전히 맴돌이 전류만으로 표현되며 공기중 전도체에서의 전자기유도 현상을 설명한다.

식 (C-1)을 식 (B-9)와 함께 식 (A-21)의 2차장 항에 대입하면

(C-2)

\begin{aligned} \int_{V} \underset{―}{\underset{―}{G}} (r, r^{'}) \cdot J_{s} (r^{'}) d r^{'} & = \int_{V} (\underset{―}{\underset{―}{S}} + \frac{1}{k_{b}^{2}} \nabla Φ) \cdot (\nabla^{'} \times ψ + k_{b}^{2} \nabla^{'} ϕ) d r^{'} \\ = \int_{V} \{\underset{―}{\underset{―}{S}} + \frac{1}{k_{b}^{2}} \nabla Φ) \cdot \nabla^{'} \times ψ + (k_{b}^{2} \underset{―}{\underset{―}{S}} + \nabla Φ) \cdot \nabla^{'} ϕ\} d r^{'} \end{aligned}

이 되므로 분모에 $k_{b}^{2}$ 이 붙어서 수치적으로 불안정성을 야기하는 항은 적분항 안의 두 번째만 남게 된다. 이 두 번째 항에 아래와 같은 벡터 정리를 적용하고,

\nabla \cdot (a b) = (\nabla \cdot a) b - a \cdot \nabla b

\begin{aligned} \nabla^{'} \cdot {(\nabla^{'} \times ψ) Φ} & = {\nabla^{'} \cdot (\nabla^{'} \times ψ)} Φ - (\nabla^{'} \times ψ) \cdot \nabla^{'} Φ \\ = - (\nabla^{'} \times ψ) \cdot \nabla^{'} Φ \end{aligned}

다음과 같이 Gauss 정리를 이용하면, 맴돌이 전류는 이상체의 경계면을 통과하지 않으므로 그 적분은 0이 된다.

(C-3)

\begin{aligned} \int_{V} \nabla Φ \cdot (\nabla^{'} \times ψ) d r^{'} & = \int_{V} (\nabla^{'} \times ψ) \cdot \nabla^{'} Φ d r^{'} \\ = - \int_{V} \nabla^{'} \cdot {(\nabla^{'} \times ψ) Φ} d r^{'} \\ = - \int_{S} \hat{n} \cdot (\nabla^{'} \times ψ) Φ d S^{'} \\ = 0 \end{aligned}

따라서, 2차장은 아래와 같이 수치적으로 안정된 형태로 표현되게 되며,

(C-4)

\int_{V} \underset{―}{\underset{―}{G}} (r, r^{'}) \cdot J_{s} (r^{'}) d r^{'} = \int_{V} {\underset{―}{\underset{―}{S}} \cdot \nabla^{'} \times ψ + (k_{b}^{2} \underset{―}{\underset{―}{S}} + \nabla Φ) \cdot \nabla^{'} ϕ} d r^{'}

결과적으로 식 (A-21)의 적분방정식은 아래와 같이 정리된다.

(C-5)

E (r) = E_{b} (r) - \hat{z} \int_{V} {\underset{―}{\underset{―}{S}} \cdot \nabla^{'} \times ψ + (k_{b}^{2} \underset{―}{\underset{―}{S}} + \nabla Φ) \cdot \nabla^{'} ϕ} d r^{'}

문제는 체적 적분방정식을 풀기 위해 이상체를 수치적으로 분할하게 될 때에 각 격자점(또는 모서리)에서 미지수는 벡터 포텐셜 $ψ$ 의 3성분과 스칼라 포텐셜 $𝜙$ 를 합쳐 4개인데 반해, 주어지는 값은 1차 전기장 $E_{b}$ 의 3성분에 불과하므로 과소결정(under-determined) 문제에 해당해서 일반적으로 해를 구할 수 없다는 데에 있다. 반면에 thin sheet 문제에서는 맴돌이 전류가 판상 전도체 면에서만 존재해서 이에 직교하는 벡터 포텐셜 하나의 성분으로 표현할 수 있고 여기에 스칼라 포텐셜을 더해 2개 미지수를 가지며, 입력 변수인 1차장도 판상 전도체의 길이 및 너비 2개 방향 성분을 가지므로 해를 구할 수 있게 된다. 이를 통해 Weidelt (1981)가 비저항이 높은 배경 매질에 대해서도 안정적으로 수치 해를 구할 수 있었고, Song et al. (2002)이 이를 확장해 0.01 Hz부터 100 MHz까지의 광대역 주파수에 걸쳐 안정적으로 적분방정식의 수치 해를 구할 수 있음을 보였다.

References

Hohmann, G. W., 1987, Numerical modeling for electromagnetic methods of geophysics, in Nabighian, M. N., Ed., Electromagnetic Methods in Applied Geophysics - Theory, Vol. 1, Soc. Expl. Geophys., 312-363.

10.1190/1.9781560802631.ch5

Jang, H., Song, Y., and Nam, M.-J., 2024, Analysis of static shift and its correction in magnetotelluric surveys, Geophys. and Geophys. Explor., 27, 129-143 (in Korean with English abstract).

Kaufman, A. A., 1992, Geophysical field theory and method, Part A - Gravitational, electric, and magnetic fields, Academic Press, Inc., 581p.

Kwon, H.-S., Song, Y., Yi, M.-J., Chung, H.-J., and Kim, K.-S., 2006, Case histories of electrical resistivity and controlled-source magnetotelluric surveys for the site investigation of tunnel construction, J. Env. Eng. Geophys., 11, 237-248.

10.2113/JEEG11.4.237

Lee, T. J., Kim, M. S., Park, I. H., Song, Y., Nam, M. J., Song, S. Y., and Yun, K.-H., 2019, Geoelectrical structure of Ulleung island, Korea, Interpretation of three-dimensional magnetotelluric data, Expl. Geophys., 50, 481-489.

10.1080/08123985.2019.1634192

Lee, T. J., Nam, M.-J., Lee, S. K., Song, Y., and Uchida, T., 2009, The Jeju dataset: Three-dimensional interpretation of MT data from mid-mountain area of Jeju island, Korea, J. Appl. Geophys., 68, 171-181.

10.1016/j.jappgeo.2008.11.006

Lee, T. J., Song, Y., and Uchida, T., 2005, Two- and three-dimensional interpretation of magnetotelluric data from Pohang geothermal site, J. Kor. Soc. Geosystem Eng., 42, 297-307 (in Korean with English abstract).

Sasaki, Y., 2004, Three-dimensional inversion of static-shifted magnetotelluric data, Earth, Planet and Space, 56, 239-248.

10.1186/BF03353406

Song, Y., Kim, H. H., and Lee, K. H., 2002, An integral equation representation of wide-band electromagnetic scattering by thin sheets, Geophysics, 67, 746-754.

10.1190/1.1484517

Tai, C.-T., 1994, Dyadic Green functions in electromagnetic theory, 2nd Ed., IEEE Press, 343p.

Torres-Verdin, C., 1991, Continuous profiling of magnetotelluric fields, Ph.D. thesis, University of California, Berkeley.

10.2172/10106102

Torres-Verdin, C. and Bostick, F. X. Jr., 1992, Principles of spatial surface electric field filtering in magnetotellurics: Electromagnetic array profiling (EMAP), Geophysics, 57, 503-622.

10.1190/1.1443273

Vozoff, K., 1991, The magnetotelluric method, in Nabighian, M. N., Ed., Electromagnetic Methods in Applied Geophysics, Vol. 2, Application, Part B, Soc. Expl. Geophys., 641-711.

10.1190/1.9781560802686.ch8

Weidelt, P., 1981, Report on dipole induction by a thin plate in a conductive halfspace with an overburden, Fed. Inst. EarthSci. And Math. Report 89727.

Geophysics and Geophysical Exploration ISSN:1229-1064(Print) 2384-051X(Online) 지구물리와 물리탐사

Preview

Static Effect in Magnetotelluric Responses: An Implication from the EM Integral Equation

ABSTRACT

MAIN

(1)

Fig. 1.

(2)

(3)

(4)

(5)

(6)

Fig. 2.

Schematic illustration showing charge accumulation at the interface between an inhomogeneity and surrounding conductive medium, and resultant distribution of the electric field for (a) conductive and (b) resistive bodies (modified from Fig. III.14 of Kaufman, 1992).

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Fig. 3.

Acknowledgements

부록: 전기장의 적분방정식

(A-1)

(A-2)

(A-3)

(A-4)

(A-5)

(A-6)

(A-7)

(A-8)

(A-9)

(A-10)

(A-11)

(A-12)

(A-13)

(A-14)

(A-15)

(A-16)

(A-17)

(A-18)

(A-19)

(A-20)

(A-21)

(A-22)

(A-23)

(A-24)

(A-25)

(B-1)

(B-2)

(B-3)

(B-4)

(B-5)

(B-6)

(B-7)

(B-8)

(B-9)

(B-10)

(B-11)

(C-1)

(C-2)

(C-3)

(C-4)

(C-5)

References